给定一个平面上$n$条水平直线和$m$条垂直直线，它们相交形成$n$行$m$列的网格，从上到下第$r$条水平直线和从左到右第$c$条垂直直线之间的交点称为格点$(r,c)$。网格中任意两个水平或垂直相邻的格点之间的线段称为一条边，每条边有一个非负整数边权。
进行$T$次询问，每次询问形式如下：
给出$k$（$T$次询问的$k$可能不同）个附加点，每个附加点位于一条从网格边缘向外出发的射线上。所有从网格边缘向外出发的射线按左上-右上-右下-左下-左上的顺序依次编号为$1$到$2n+2m$，如下图：

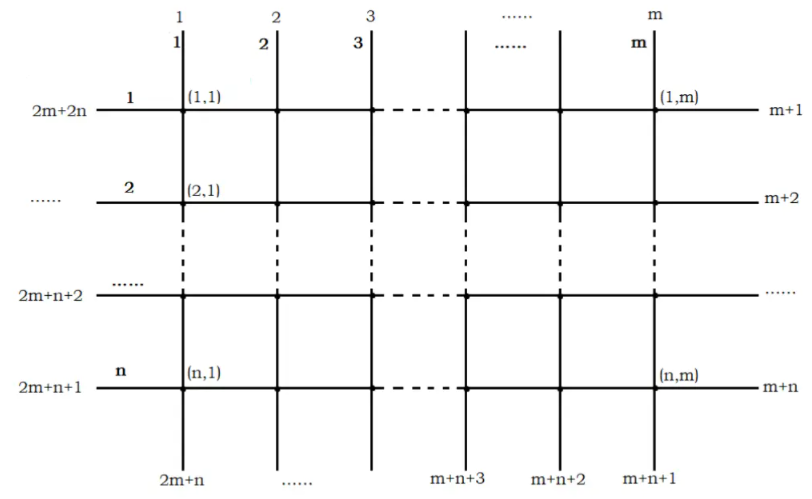
对于每次询问，不同附加点所在的射线互不相同。每个附加点和最近的格点之间的线段也称为一条边，也有非负整数边权（注意，在角上的格点有可能和两个附加点同时相连）。
给定每个附加点的颜色（黑色或者白色），请你将网格内每个格点的颜色染成黑白二者之一，并使得所有两端颜色不同的边的边权和最小。请输出这个最小的边权和。

第一行，三个正整数$n,m,T$，分别表示水平、垂直直线的数量，以及询问次数。
接下来$n-1$行，每行$m$个非负整数。其中第$i$行的第$j$个非负整数${x_1}_{i,j}$表示$(i,j)$和$(i+1,j)$间的边权。
接下来$n$行，每行$m-1$个非负整数。其中第$i$行的第$j$个非负整数${x_2}_{i,j}$表示$(i,j)$和$(i,j+1)$间的边权。
接下来依次输入$T$组询问。第$i$组询问开头为一行一个正整数$k_i$表示这次询问附加点的总数。接下来$k_i$行每行三个非负整数。其中第$j$行依次为${x_3}_{i,j},p_{i,j},t_{i,j}$表示第$j$个附加点和相邻格点之间的边权、所在的射线编号以及附加点颜色（$0$为白色，$1$为黑色）。保证同一组询问内$p_{i,j}$互不相同。
每行的多个整数由空格分隔。

输出$T$行，第$i$行输出一个非负整数，表示第 次询问染色之后两端颜色不同的边权和的最小值。

最优方案：$(1,3),(1,2),(2,3)$为黑色；$(1,1),(2,1),(2,2)$为白色。
数据范围与提示

对于所有数据，$2\leqslant n,m\leqslant 500,1\leqslant T\leqslant 50,1\leqslant k_i\leqslant min\{2(n+m),50\},1\leqslant \sum _{T}^{i=1} k_i\leqslant 50,0\leqslant x\leqslant 10^6,1\leqslant p\leqslant 2(n+m),t\in \{0,1\}$。
保证对于每个$i \in [1,T]$，$p_{i,j}$互不相同。