E国有n个城市，编号为1至n。为了让城市之间的来往更加便利，E国的交通部想在n个城市间建造一些虫洞。每条虫洞是一条单向的从某个城市到另一个城市的通道。允许通道的起点和终点是同一个城市，也允许两个城市之间有多个虫洞连接。
为了区分虫洞的建造时间，交通部给每一条虫洞一个正整数的编号。
我们称一种虫洞的建造方案是好的，若它满足如下四个条件：
(1)存在一个非负整数d使得每个城市恰好是d条虫洞的起点，也恰好是d条虫洞的终点。
(2)对于每个城市而言，在以它为起点的虫洞的编号中，1到d恰好各出现一次。
(3)对于每个城市而言，在以它为终点的虫洞的编号中，1到d恰好各出现一次。
(4)任意选取一个城市u和正整数$1≤j_1,j_2≤d$。设从u出发，先经过一次编号为
j1的虫洞，再经过一次编号为j2的虫洞，到达城市v1。设从u出发，先经过一次编号为j2的虫洞，再经过一次编号为j1的虫洞，到达城市v2。则条件v1=v2必定满足。
特别地，不建造任何虫洞的方案也是好的。
现在，建造师已建造了mn条虫洞，且给了它们1∼m的编号，此时这样的建造方案是好的。他想要新建造kn条虫洞，并给它们(m+1)∼(m+k)的编号。他必须保证这(m+k)n条虫洞形成的建造方案仍然是好的。他想知道有多少种新建造kn条虫洞的方法，使得这(m+k)n条虫洞形成的建造方案是好的。
由于答案很大，你只需要求出方案数除以998244353的余数。

输入的第一行四个非负整数c,n,m,k，其中c表示测试点编号。样例中的c表示该样例的数据范围与第c个测试点的数据范围相同。
接下来nm行，每行三个正整数u,v,w，表示一条编号为w的，起点为u号城市，终点为v号城市的虫洞。

输出一行整数，表示方案数除以998244353的余数。

【样例1解释】
在该组样例中，已经建造的编号为1的虫洞为1→2,2→1,3→4,4→3。为了使8条虫洞形成的建造方案是好的，新建造的编号为2的虫洞可能有8种情形：
(1)1→1,2→2,3→3,4→4
(2)1→1,2→2,3→4,4→3
(3)1→2,2→1,3→3,4→4
(4)1→2,2→1,3→4,4→3
(5)1→3,2→4,3→1,4→2
(6)1→3,2→4,3→2,4→1
(7)1→4,2→3,3→1,4→2
(8)1→4,2→3,3→2,4→1
【样例2】
第2个测试点的限制条件。
【样例3】
第5个测试点的限制条件。
【样例4】
第7个测试点的限制条件。
【样例5】
该样例的c=9，它满足第9个测试点的限制条件。
【样例6】
该样例的c=11，它满足第11个测试点的限制条件。
【样例7】
该样例的c=15，它满足第15个测试点的限制条件。
【样例8】
该样例的c=17，它满足第17个测试点的限制条件。
【样例9】
该样例的c=20，它满足第20个测试点的限制条件。
【样例10】
该样例的c=22，它满足第22个测试点的限制条件。
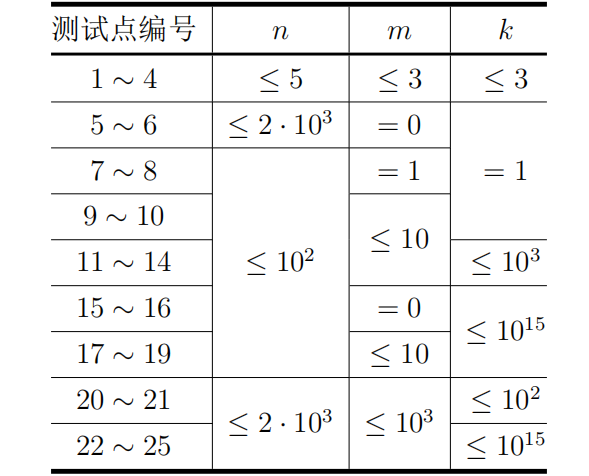
【子任务】
对于所有测试点，
•$1≤n≤2·10^3，0≤m≤10^3，1≤k≤10^{15}$；
•$1≤u,v≤n，1≤w≤m$；
•保证初始建造的mn条虫洞构成一个好的建造方案。

本题部分测试点输入规模较大，我们推荐你使用较为快速的读入方式。