小Z手里有很多很多三维弹球，为了把它们收集起来，她设计了一个容器。

这个容器可以看作一个有根树的结构，每个节点的标号为从1到n。每个节点可以是空的或者可以容纳一个弹球。一开始，所有节点都是空的。

当小Z开始收集弹球的时候，可能会产生以下两种操作：

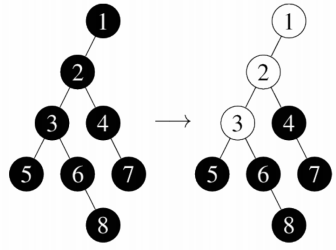
1. 往容器中依次放 x 个球。球被依次放进根节点，只要这个球的下方有空节点，它就会往下掉落。如果有多个空节点，那么球会选择子树中的最小节点编号最小的子节点掉落。所以如果一个球往下掉落多次，它将会在第一层做一次选择。比如我们往下图这个容器中放两个球，它们将依次落在1号和3号节点上。第一个球从4号落到了3号，因为3号是空的，且以3号节点为根的子树中最小节点编号是1（比2更小），然后它从3号落到了1号节点。第二个球从4号落到3号，然后停住了。

2. 从 x 号节点上拿走球。因为小 Z 在整理的过程中发现 x 号节点上的球很好玩，于是把它拿了出来，这就会导致它上面的球（如果有的话）可能会往下掉落。只要一个空节点的父亲节点有球，那么这个球就会向下掉落。比如我们从下图容器中依次取走5号、7号和8号节点的球，最终1号、2号和3号节点将变为空节点。移走5号节点的球时，3号、2号和1号节点的球依次掉落；移走6号节点的球时，3号和2号节点的球依次掉落；移走8号节点时，6号和3号节点的球依次掉落。

第一行包含三个整数 n,q 和testID，分别表示树的节点个数、操作数和测试点编号。

第二行包含 n 个整数 f_i，表示 i 的父亲节点。如果 f_i = 0，说明 i 是根节点。

接下来 q 行，每行两个数 type 和 x，意义见题目描述。

输入数据保证所有操作均合法，即加入球的个数不会超过空位的个数，也不会从一个空节点移除球。

对于每个操作 1，输出最后一个加入的球所在的位置；

对于每个操作 2，输出移除该球后会引起多少个球下落。

样例解释

加入 8 个球所以第 8 个球的位置是 1 号节点，剩下三个操作 2 的解释见题面描述。

数据规模与约定

记特征 A 表示“只有一次操作 1”，特征 B 表示“操作 2 不会造成球的下落”。

“随机构造”的树是指对于 i(i > 1) 号节点，i 的父亲节点从 [1, i − 1] 中等概率随机选取。