Alice 拥有一座迷宫，这座迷宫可以抽象成一棵拥有$2^n$个叶节点的满二叉树，总节点数目为（$2^{n+1}-1$)，依次编号为 1 ～（$2^{n+1}-1$)。其中编号为 2～（$2^{n+1}-1$）的是叶节点，编号为1～（$2^2-1$）的是非叶节点，且非叶节点$1\leq u\leq（2^2-1）$的左儿子编号为$2u$，右儿子编号为$(2u+1)$。
每个非叶节点都有一个石像守卫，初始时，所有石像守卫均在沉睡。唤醒$u$点的石像守卫需要$w_u$的魔力值。
每个叶节点都有一个符文，点的符文记作$q_u$。保证$q_{2n},q_{2n+1},\cdots,q_{2^{n+1}-1}$构成$1～2^n$的排列。
探险者初始时持有空序列$Q$，从节点1出发，按照如下规则行动：

• 到达叶节点时，将点的符文$\alpha$ 添加到序列$Q$的末尾，然后返回父节点。
• 到达非叶节点$u$时:
• 若该点的石像守卫已被唤醒，则只能先前往左儿子，（从左儿子返回后）再前往右儿子，（从右儿子返回后）最后返回父节点。
• 若该点的石像守卫在沉睡，可以在以下二者中任选其一:
  *先前往左儿子，再前往右儿子，最后返回父节点。
  *先前往右儿子，再前往左儿子，最后返回父节点。

返回节点 1 时，探险结束。可以证明，探险者一定访问每个叶节点各一次，故此时 $Q$ 的长度为 $2^n$。
探险者Bob 准备进入迷宫，他希望探险结束时的 Q 的字典序越小越好，与之相对，Alice 希望Q 的字典序越大越好。
在Bob 出发之前，Alice 可以选择一些魔力值花费之和不超过K 的石像守卫，并唤醒它们。Bob 出发时，他能够知道 Alice 唤醒了哪些神像。若双方都采取最优策略，求序列Q 的最终取值。
对于两个长度为 $2^n$ 的序列 $Q_1,Q_2$，称 $Q_1$ 字典序小于 $Q_2$ 当且仅当以下条件成立：

• $\exists i \in [1,2^n]$ 满足以下两个条件：
  $\forall 1 \leq j < i , Q_{1,j} = Q_{2,,j}$；
  $Q_{1,i} < Q_{2,i}$。

本题有多组测试数据。.输入的第一行包含一个正整数 $T$，表示测试数据组数。
接下来依次 $T$ 组测试数据。对于每组测试数据：

• 第一行两个整数 $n, K$ 表示迷宫规模和 Alice 可用于唤醒石像守卫的魔力值上限。
• 第二行 $(2^n - 1)$ 个整数 $w_1, w_2, \cdots, w_{2^n - 1}$ 表示唤醒各个石像守卫耗费的魔力值。
• 第三行 $2^n$ 个整数 $q_{2^n}, q_{2^{n+1}}, \cdots, q_{2^{n+1}-1}$ 表示各个叶节点上的符文。

对于每组数据，输出一行 $2^n$ 个整数 $Q_1, Q_2, \cdots, Q_{2^n}$，表示双方都采取最优策略的情况下，序列 $Q$ 的最终取值。

【样例 1 解释】

• 第一组数据中，Alice 无法唤醒石像守卫，Bob 可以选择先访问叶节点 3，再访问叶节点 2，得 $Q = \{1, 2\}$。
• 第二组数据中，Alice 可以唤醒节点 1 的石像守卫，Bob 只能先访问叶节点 2，再访问叶节点 3，得 $Q = \{2, 1\}$。
• 第三组数据中，Alice 的最优策略是唤醒节点 5, 6 的石像守卫。

【样例 2】
见附件中的 maze/maze2.in 与 maze/maze2.ans。该组数据满足特殊性质 A。

【样例 3】
见附件中的 maze/maze3.in 与 maze/maze3.ans。该组数据满足特殊性质 B。

【样例 4】
见附件中的 maze/maze4.in 与 maze/maze4.ans。

【样例 5】
见附件中的 maze/maze5.in 与 maze/maze5.ans。

【子任务】
设 $\sum 2^n$ 表示单个测试点中所有测试数据的 $2^n$ 的和。对于所有测试数据，保证

• $1 \leq T \leq 100$;
• $1 \leq n \leq 16$, $1 \leq \sum 2^n \leq 10^5$;
• $0 \leq K \leq 10^{12}$;
• $\forall 1 \leq u \leq (2^n - 1)$, $0 \leq w_u \leq 10^{12}$;
• $q_{2^n}, q_{2^{n+1}}, \cdots, q_{2^{n+1}-1}$ 构成 $1 \sim 2^n$ 的排列。
  
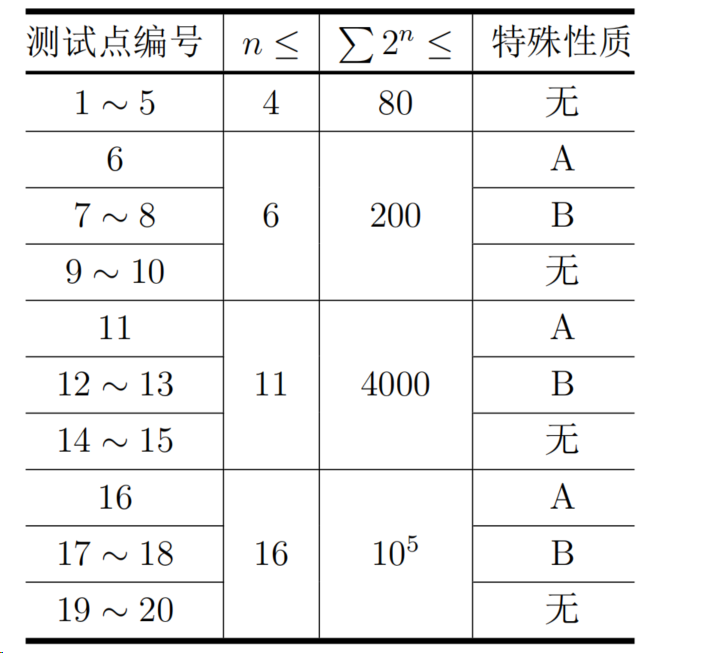
  特殊性质 A: $\forall 2^n \leq v \leq (2^{n+1} - 1)$, $q_v = (2^{n+1} - v)$。
  特殊性质 B: $\forall 1 \leq u \leq (2^n - 1)$, $w_u = 1$。