公元 9012 年，Z 市的航空基地计划举行一场特技飞行表演。表演的场地可以看作一个二维平面直角坐标系，其中横坐标代表着水平位置，纵坐标代表着飞行高度。
  在最初的计划中，这 $n$ 架飞机首先会飞行到起点 $x=x_{st}$ 处，其中第 $i$ 架飞机在起点处的高度为 $y_{i,0}$。它们的目标是终点 $x = x_{ed}$ 处，其中第 $i$ 架飞机在终点处的高度应为 $y_{i,1}$。因此，每架飞机可以看作坐标系中的一个点，它的航线是从 $(x_{st}, y_{i,0})$ 出发、到 $(x_{ed},y_{i,1})$ 结束的一条线段，如下图所示。

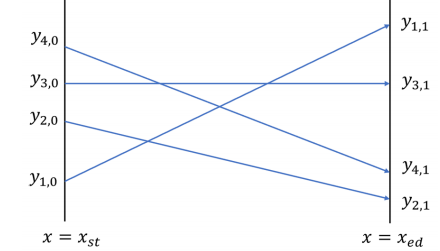
  这 $n$ 架飞机同时出发且始终保持一定的对地速度。因此，对于任意两条交叉的航线（线段），对应的两架飞机必然会同时到达交点处——这就是它们进行特技表演的时刻。它们将会偏转机翼，展现以极近的距离“擦身而过”特技，然后继续保持各自的航线。
  航空基地最近还研究了一种新的特技“对向交换”。当两架飞机到达交点处时，之前正在下降的那架立即转为执行抬升动作，之前正在上升的那架则执行一次空翻，两架飞机一上一下、机腹对机腹，同样以极近的距离经过交点，然后互相交换接下来的航线。
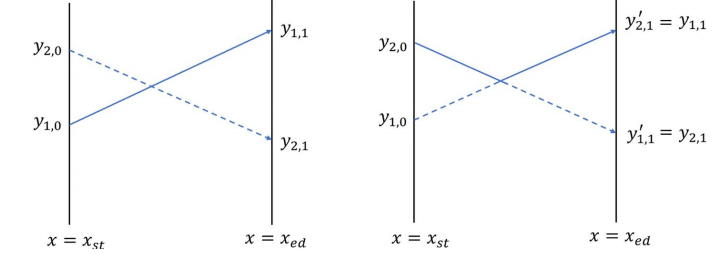
  我们不必关心特技动作在物理上究竟是如何实现的，飞机仍然看作一个点，在两种特技动作下，航线的变化如下图所示（$y^{'}_{i,1}$ 表示交换航线后第 $i$ 架飞机在终点的新高度）。容易发现，“对向交换”会使它们的航线变为折线，并保持它们在纵坐标上的相对顺序；而“擦身而过”会改变它们在纵坐标上的相对顺序。

  现在，观看表演的嘉宾团提出了一个苛刻的要求——在终点 $x=x_{ed}$ 处，按照高度排序，$m$ 架飞机的相对顺序必须与 $x=x_{st}$ 处的相对顺序一致。嘉宾团还给“对向交换”特技和“擦身而过”特技分别评定了难度系数 $a$ 和 $b$，每次“对向交换”特技可以获得 $a$ 的分数，每次“擦身而过”特技可以获得 $b$ 的分数。
  除此以外，嘉宾团共有 $k$ 名成员，第 $i$ 名成员会乘热气球停留在位置 $(p_i,q_i)$ 处，具有 $r_i$ 的观测距离，可以观测到区域 $|x-p_i|+|y-q_i|\leq r_i$ 里的所有特技。若某个交点处的特技被一名或多名嘉宾观测到，则可以获得 $c$ 的额外加分。注意：特技无论是否被观测到，均可以获得 $a$ 或者 $b$ 的得分。

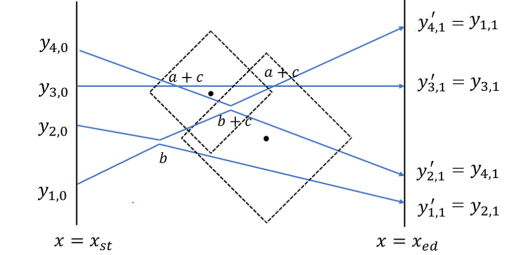
  在这次的剧情里，你成为了 $Z$ 市航空基地的规划员，你可以决定在每个交点处是执行“对向交换”还是“擦身而过”。你被要求在保证嘉宾团要求的前提下，计算整个特技表演的可能得到的最低和最高分数。

  第一行包含六个非负整数 $n,a,b,c,x_{st},x_{ed}$，分别表示航线（线段）总数、“对向交换”特技的得分、“擦身而过”特技的得分、观测对表演的额外加分、飞行起点的横坐标、飞行终点的横坐标。
  第二行包含 $n$ 个非负整数 $y_{i,0}$，其中第 $i$ 个数表示第 $i$ 条航线起点的纵坐标，保证按照从低到高的顺序给出，即 $y_{i,0}<y_{i+1,0}$。
  第三行包含 $n$ 个非负整数 $y_{i,1}$，其中第 $i$ 个数表示第 $i$ 条航线终点的纵坐标。
  第四行包含一个非负整数 $k$，表示嘉宾的数量。
  接下来 $k$ 行每行三个非负整数 $p_i,q_i,r_i$，分别表示第 $i$ 名嘉宾所在位置的横、纵坐标与观测距离。
  输入数据对于所有航线（线段）在直线 $x=x_{st}$ 和 $x=x_{ed}$ 之间的交点总数也有一些限制，详见“数据规模与约定”。

  输出只有一行，包含两个整数，表示整个特技飞行表演的可能得到的最低和得最高分数，中间用一个空格隔开。

样例说明 1
  该样例的航线就是题目描述的图中所画的情况，只是嘉宾所在的位置稍有不同。
  最低得分的表演方案是在所有交点处均采用“对向交换”特技，得分 $4a+3c=13$。
  最高得分的表演方案与题目描述的图中所画的情况一致，得分 $2a+2b+3c=15$。
数据规模与约定