【题目背景】
    本题中合法括号串的定义如下：
    $()$ 是合法括号串。
    如果 $A$ 是合法括号串，则 $(A)$ 是合法括号串。
    如果 $A$，$B$ 是合法括号串，则 $AB$ 是合法括号串。
    本题中子串与不同的子串的定义如下：
    字符串 $S$ 的子串是 $S$ 中连续的任意个字符组成的字符串。$S$ 的子串可用起始位置 $l$ 与终止位置 $r$ 来表示，记为 $S (l, r)$（$1\leq l\leq r\leq |S||S|$ 表示 $S$ 的长度）。
    $S$ 的两个子串视作不同当且仅当它们在 $S$ 中的位置不同，即 $l$ 不同或 $r$ 不同。
    题目描述
    一个大小为 $n$ 的树包含 $n$ 个结点和 $n−1$ 条边，每条边连接两个结点，且任意两个结点间有且仅有一条简单路径互相可达。
    小 $Q$ 是一个充满好奇心的小朋友，有一天他在上学的路上碰见了一个大小为 $n$ 的树，树上结点从 $1 ∼ n$ 编号，1 号结点为树的根。除 1 号结点外，每个结点有一个父亲结点，$u(2≤u≤u)$号结点的父亲为 $f_u(1≤f_u<u)$号结点。
    小 $Q$ 发现这个树的每个结点上恰有一个括号，可能是( 或)。小 $Q$ 定义 $s_i$ 为：将根结点到 $i$ 号结点的简单路径上的括号，按结点经过顺序依次排列组成的字符串。
    显然 $s_i$ 是个括号串，但不一定是合法括号串，因此现在小 $Q$ 想对所有的 $i(1≤i≤n)$求出，$s_i$ 中有多少个互不相同的子串是合法括号串。
    这个问题难倒了小 $Q$，他只好向你求助。设 $s_i$ 共有 $k_i$ 个不同子串是合法括号串， 你只需要告诉小 $Q$ 所有 $i×k_i$ 的异或和，即：
    $(1×k_1) xor (2×k_2) xor (3×k_3) xor ⋯ xor (n×k_n)$
    其中 $xor$ 是位异或运算。

第一行一个整数 $n$，表示树的大小。
    第二行一个长为 $n$ 的由 $’(’$ 与 $’)’$ 组成的括号串，第 $i$ 个括号表示 $i$ 号结点上的括号。
    第三行包含 $n−1$ 个整数，第 $i(1 ≤ i < n)$ 个整数表示 $i+ 1$ 号结点的父亲编号 $f_{i+1}$。

仅一行一个整数表示答案。

【样例解释】
    树的形态如下图：

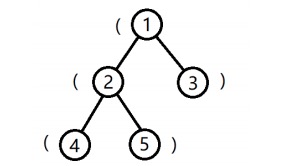
将根到 1 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 (，子串是合法括号串的个数为 0。

将根到 2 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 ((，子串是合法括号串的个数为 0。

将根到 3 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 ()，子串是合法括号串的个数为 1。

将根到 4 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 (((，子串是合法括号串的个数为 0。

将根到 5 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 (()，子串是合法括号串的个数为 1。

【数据范围】