Emiya 是个擅长做菜的高中生，他共掌握 $n$ 种烹饪方法，且会使用 $m$ 种主要食材做菜。为了方便叙述，我们对烹饪方法从 $1∼n$ 编号，对主要食材从 $1∼m$ 编号。
    Emiya 做的每道菜都将使用恰好一种烹饪方法与恰好一种主要食材。更具体地，Emiya 会做 $a_{i,j}$ 道不同的使用烹饪方法 $i$ 和主要食材 $j$ 的菜$(1≤i≤n,1≤j≤m)$，这也意味着 Emiya 总共会做道$\sum_{i=1}^{n}\sum_{j=1}^{m}a_{i,j}$不同的菜。
    Emiya 今天要准备一桌饭招待 Yazid 和 Rin 这对好朋友，然而三个人对菜的搭配有不同的要求，更具体地，对于一种包含 $k$ 道菜的搭配方案而言：
    Emiya 不会让大家饿肚子，所以将做至少一道菜，即 $k≥1$
    Rin 希望品尝不同烹饪方法做出的菜，因此她要求每道菜的烹饪方法互不相同
    Yazid 不希望品尝太多同一食材做出的菜，因此他要求每种主要食材至多在一半的菜（即 $⌊\frac{k}{2}⌋$ 道菜）中被使用
    这里的 $⌊x⌋$ 为下取整函数，表示不超过 $x$ 的最大整数。
    这些要求难不倒 Emiya，但他想知道共有多少种不同的符合要求的搭配方案。两种方案不同，当且仅当存在至少一道菜在一种方案中出现，而不在另一种方案中出现。
    Emiya 找到了你，请你帮他计算，你只需要告诉他符合所有要求的搭配方案数对质数 $998, 244, 353$ 取模的结果。

第 1 行两个用单个空格隔开的整数 $n$, $m$。
    第 2 行至第 $n + 1$ 行，每行 $m$ 个用单个空格隔开的整数，其中第 $i + 1$ 行的 m 个数依次为 $a_{i,1}, a_{i,2}, . . . , a_{i,m}$。

仅一行一个整数，表示所求方案数对 $998, 244, 353$ 取模的结果。

【样例 1 解释】
    由于在这个样例中，对于每组 $i$, $j$，Emiya 都最多只会做一道菜，因此我们直接通过给出烹饪方法、主要食材的编号来描述一道菜。
    符合要求的方案包括：
    • 做一道用烹饪方法 1、主要食材 1 的菜和一道用烹饪方法 2、主要食材 2 的菜
    • 做一道用烹饪方法 1、主要食材 1 的菜和一道用烹饪方法 2、主要食材 3 的菜
    • 做一道用烹饪方法 1、主要食材 3 的菜和一道用烹饪方法 2、主要食材 2 的菜
    因此输出结果为 $3\ mod\ 998, 244, 353 = 3$。
    需要注意的是，所有只包含一道菜的方案都是不符合要求的，因为唯一的主要食材在超过一半的菜中出现，这不满足 Yazid 的要求。
    【样例 2 解释】
    Emiya 必须至少做 2 道菜。
    做 2 道菜的符合要求的方案数为 100。
    做 3 道菜的符合要求的方案数为 90。 因此符合要求的方案数为 $100 + 90 = 190$。
    【数据范围】

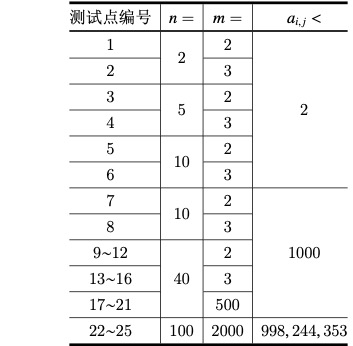
    对于所有测试点，保证 $1 ≤ n ≤ 100$，$1 ≤ m ≤ 2000$，$0 ≤ a_{i,j} < 998,244,353$。