小简单正在学习离散数学，今天的内容是图论基础，在课上他做了如下两条笔记:
    1. 一个大小为 $n$ 的树由 $n$ 个结点与 $n − 1$ 条无向边构成，且满足任意两个结点间有且仅有一条简单路径。在树中删去一个结点及与它关联的边，树将分裂为若干个子树;而在树中删去一条边(保留关联结点，下同)，树将分裂为恰好两个子树。
    2. 对于一个大小为 $n$ 的树与任意一个树中结点 $c$，称 $c$ 是该树的重心当且仅当在树中删去 $c$ 及与它关联的边后，分裂出的所有子树的大小均不超过 $⌊\frac{n}{2}⌋$ (其中 $⌊x⌋$ 是下取整函数)。对于包含至少一个结点的树，它的重心只可能有 $1$ 或 $2$ 个。
    课后老师给出了一个大小为 $n$ 的树 $S$ ，树中结点从 $1 ∼ n$ 编号。小简单的课后作业是求出 $S$ 单独删去每条边后，分裂出的两个子树的重心编号和之和。即:

    上式中，$E$ 表示树 $S$ 的边集，$(u, v)$ 表示一条连接 $u$ 号点和 $v$ 号点的边。$S_{u}^{′}$ 与 $S_{v}^{′}$ 分别表示树 $S$ 删去边 $(u, v)$ 后，$u$ 号点与 $v$ 号点所在的被分裂出的子树。
    小简单觉得作业并不简单，只好向你求助，请你教教他。

本题输入包含多组测试数据。
    第一行一个整数 $T$ 表示数据组数。
    接下来依次给出每组输入数据，对于每组数据:
    第一行一个整数 $n$ 表示树 $S$ 的大小。
    接下来 $n − 1$ 行，每行两个以空格分隔的整数 $u_i$, $v_i$，表示树中的一条边 $(u_i, v_i)$。

共 $T$ 行，每行一个整数，第 $i$ 行的整数表示:第 $i$ 组数据给出的树单独删去每条边 后，分裂出的两个子树的重心编号和之和。

【样例解释】
    对于第一组数据：
    删去边 $(1, 2)$，$1$ 号点所在子树重心编号为 $\{1\}$，$2$ 号点所在子树重心编号为 $\{2, 3\}$。
    删去边 $(2, 3)$，$2$ 号点所在子树重心编号为 $\{2\}$，$3$ 号点所在子树重心编号为 $\{3, 5\}$。
    删去边 $(2, 4)$，$2$ 号点所在子树重心编号为 $\{2, 3\}$，$4$ 号点所在子树重心编号为 $\{4\}$。
    删去边 $(3, 5)$，$3$ 号点所在子树重心编号为 $\{2\}$，$5$ 号点所在子树重心编号为 $\{5\}$。
    因此答案为 $1 + 2 + 3 + 2 + 3 + 5 + 2 + 3 + 4 + 2 + 5 = 32$。
    【数据范围】

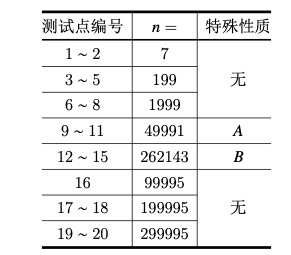
    表中特殊性质一栏，两个变量的含义为存在一个 $1 ∼ n$ 的排列 $p_i(1 ≤ i ≤ n)$，使得:
    $A$:树的形态是一条链。即 $∀1 ≤ i < n$，存在一条边 $(p_i, p_{i+1})$。
    $B$:树的形态是一个完美二叉树。即 $∀1 ≤ i ≤ \frac{n-1}{2}$，存在两条边 $(p_i, p_{2i})$ 与 $(p_i, p_{2i+1})$。
    对于所有测试点:$1 ≤ T ≤ 5$ , $1 ≤ u_i, v_i ≤ n$。保证给出的图是一个树。