P9170 [NOI2020统一省选]组合数问题
描述
众所周知,小葱同学擅长计算,尤其擅长计算组合数。小葱现在希望你计算
的值。其中 为给定的整数, 为给定的一个 次多项式。 为组合数,其值为
输入
第一行四个非负整数 。
第二行 个整数,分别代表 。
输出
仅一行一个整数表示答案。
样例输入 1
5 1 10007 2
0 0 1
样例输出 1
240
样例输入 2
996 233 998244353 5 5 4 13 16 20 15
样例输出 2
869469289
提示
【样例 1 解释】
。
,故 恒为 1,乘积中的该项可以忽略。
,,,,。
最终答案为:
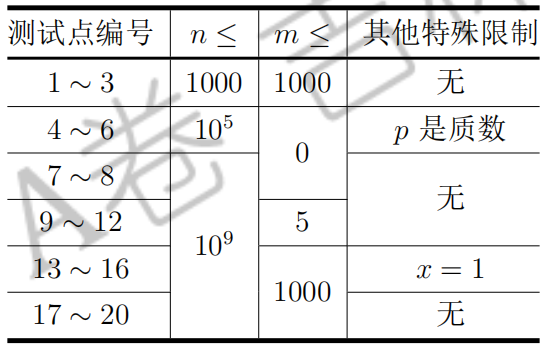
【数据范围】
对于所有测试数据:。
每个测试点的具体限制见下表: