笠笠和伦伦来到了一家魔法商店，这家商店内有 n 件礼品，礼品从 1 ∼ n 编号，i号礼品的魅力值为 $c_i$，价格为 $v_i$。
两人希望购买一些礼品，但他们的要求比较奇怪：假设购买到的礼品集合为 $S ={s_1, s_2, · · · , s_p}(1 ≤ si ≤ n)$，两人要求对于 S 中任意的非空子集 $T = \{t_1, t_2, · · · , t_q\}$，它包含的所有礼品的魅力值异或和都不为零，即$c_{t_1} ⊕ c_{t_2} ⊕ · · · ⊕ c_{t_q} = 0$，其中 ⊕ 是异或运算。在此基础上，两人还要求购买到的礼品数尽可能多。
例如：$c_1 = 1，c_2 = 2，c_3 = 5，c_4 = 6，c_5 = 7$。则 $S_1 = \{2, 3, 5\}$ 不符合要求，因为$c_2 ⊕ c_3 ⊕ c_5 = 0$。$S_2 = \{1, 2, 3\}$ 与 $S_3 = \{2, 4, 5\}$ 符合要求，其任意非空子集的异或和都不为零。$S_4 = \{1, 2\}$ 不符合要求，因为其包含的礼品数不是最多的。
满足两人要求的礼品集合可能很多，因此商店老板为两人挑选出了两个符合要求的礼品集合 A 与 B（显然它们所含的礼品数相同），伦伦喜欢集合 A，但笠笠更喜欢集合B。为了笠笠同意购买集合 A，伦伦决定使用魔法改变礼品价格。更具体地，伦伦能花费 $(x - v_i)^2$ 的魔力值，将 i 号礼品的价格改为任意整数 $x$，每件礼品只能被改价一次。
伦伦希望改价后 A 是所有符合要求的礼品集合之中价格总和最小的，且 B 是所有符合要求的礼品集合之中价格总和最大的（一个礼品集合的价格总和为它包含的所有礼品的价格之和）。现在请你帮伦伦计算，他至少要花费多少魔力值才能完成他的目标。

第一行两个整数 $n,m$，分别表示总礼品数与礼品集合 $A(B)$包含的礼品数。
第二行 n 个整数 $c_i$，第 i 个整数表示 i 号礼品的魅力值。
第三行 n 个整数 $v_i$，第 i 个整数表示 i 号礼品的价格。
第四行 m 个整数 $a_i$，表示礼品集合 A 包含的礼品的编号。数据保证 $a_i$ 两两不同。
第五行 m 个整数 $b_i$，表示礼品集合 B 包含的礼品的编号。数据保证 $b_i$ 两两不同。
数据保证 $1 ≤ a_i$, $b_i ≤ n$，且礼品集合 A 和 B 均符合两人的要求。

仅一行一个整数，表示伦伦至少需要花费的魔力值。

【样例解释】
符合条件的礼品集合有：{1, 2, 3}，{1, 2, 4}，{1, 2, 5}，{1, 3, 4}，{1, 3, 5}，{2, 3, 4}， {2, 4, 5}，{3, 4, 5}。
一个最优的改价方案为：$c_1 = c_2 = c_4 = c_5 = 3，c_3 = 2$。
【数据范围】
对于所有测试数据：$1 ≤ n ≤ 1000，1 ≤ m ≤ 64，1 ≤ c_i < 2^64，0 ≤ v_i ≤ 10^6$。
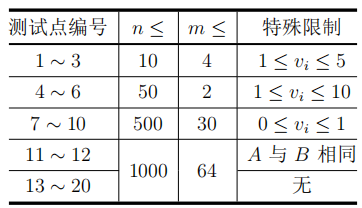
每个测试点的具体限制见下表：